How To Report Skewness And Kurtosis

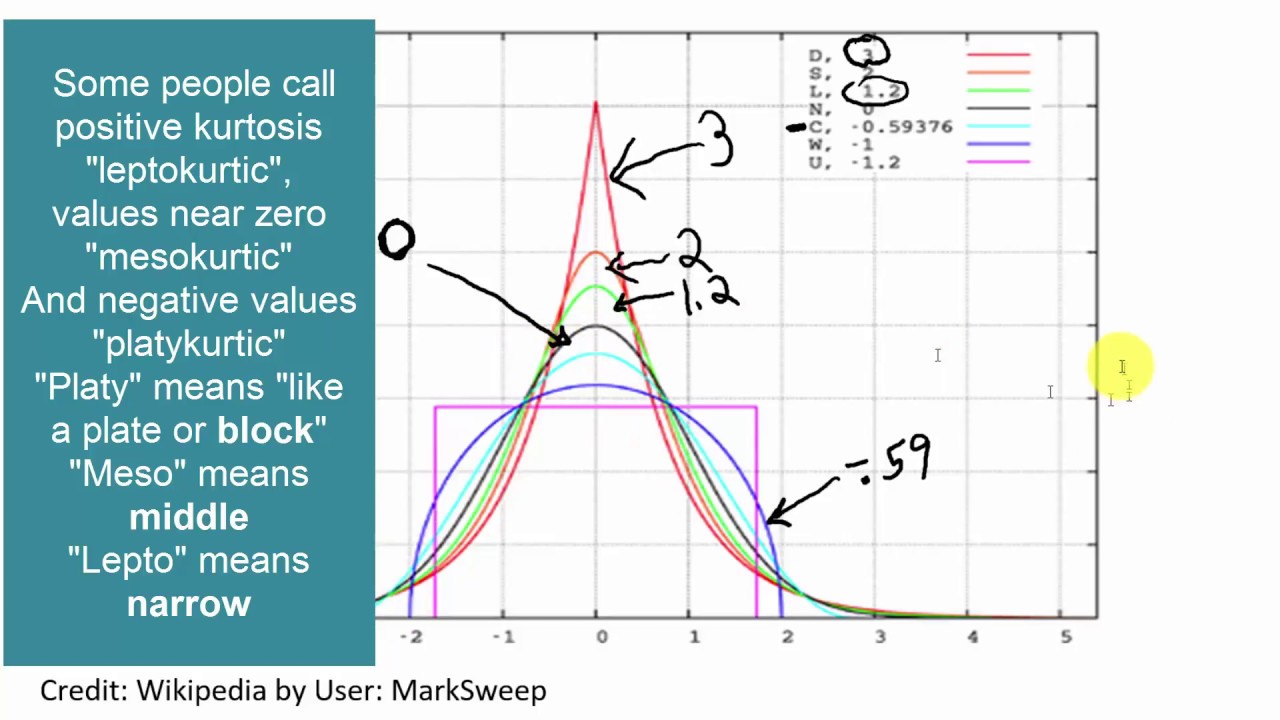
Figure 1 examples of skewness and kurtosis.

How to report skewness and kurtosis. Skewness and kurtosis a fundamental task in many statistical analyses is to characterize the location and variability of a data set. M 19 2 sd 2 32. Here x is the sample mean. If it s unimodal has just one peak like most data sets the next thing you notice is whether it s symmetric or skewed to one side.

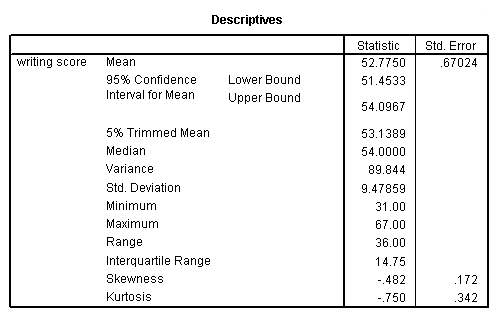
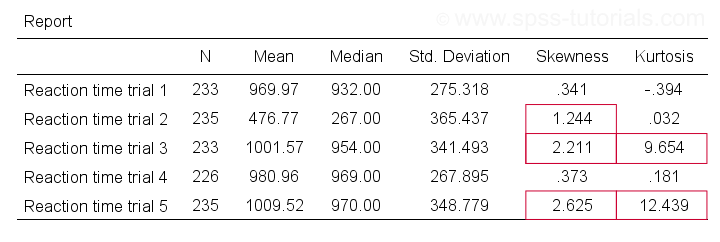
Non normally distributed with skewness of 1 87 se 0 05 and kurtosis of 3 93 se 0 10 participants were 98 men and 132 women aged 17 to 25 years men. Kurtosis is a measure of whether the distribution is too peaked a very narrow distribution with most of the responses in the center hair et al 2017 p. Kurtosis is sensitive to departures from normality on the tails. Tails of the distribution of data and therefore provides an indication of the presence of outliers.

Peak is higher and sharper than mesokurtic which means that data are heavy tailed or profusion of outliers. Kurtosis provides a measurement about the extremities i e. Outliers stretch the horizontal axis of the histogram graph which makes the bulk of the data appear in a narrow skinny vertical range thereby giving the skinniness of a leptokurtic distribution. If the bulk of the data is at the left and the right tail is longer we say that the distribution is skewed right or positively.

Non parametric tests do not report means and standard deviations for non parametric tests. Skew r and skew p r ignore any empty cells or cells with non numeric values. Because of the 4th power smaller values of centralized values y i µ in the above equation are greatly de emphasized. Also high kurtosis not imply pointiness or peakedness you can have a distribution that is perfectly flat over 99 99 of the potentially observable data eg returns having arbitrarily high kurtosis.

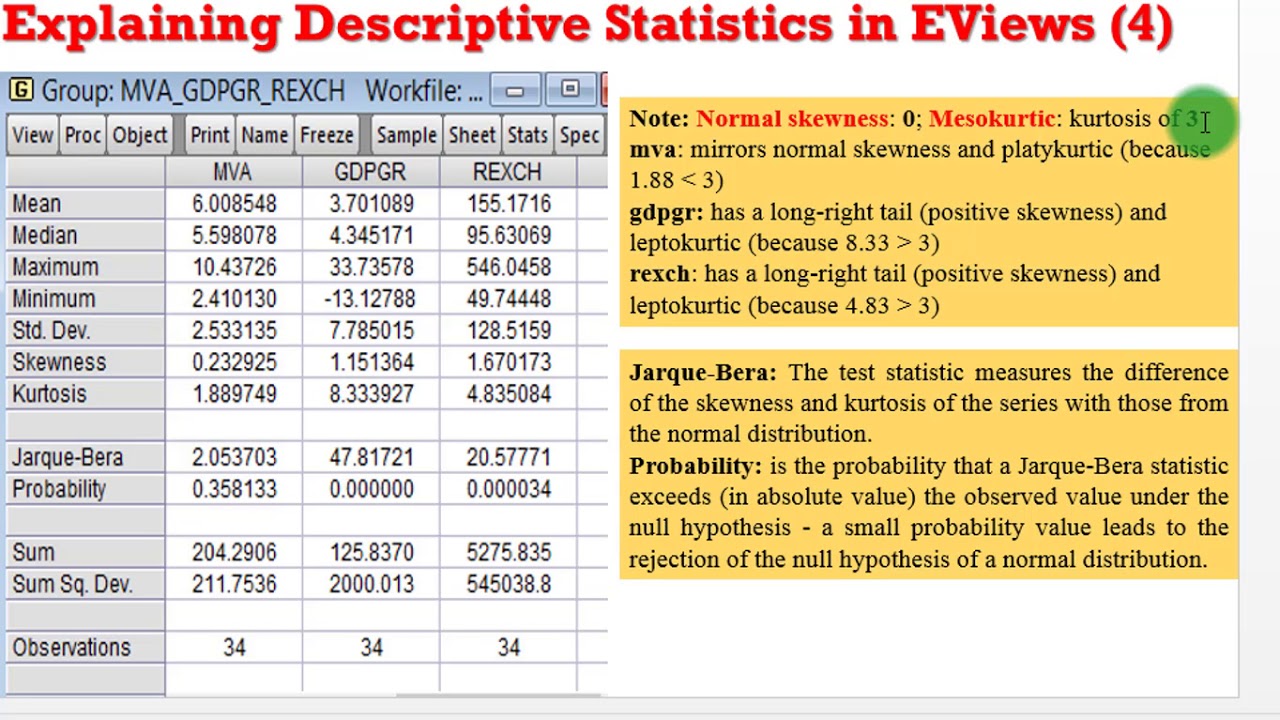
Kurtosis tells you the height and sharpness of the central peak relative to that of a standard bell curve. Distribution is longer tails are fatter. A further characterization of the data includes skewness and kurtosis. Because it is the fourth moment kurtosis is always positive.

Leptokurtic kurtosis 3. Skewness is a measure of symmetry or more precisely the lack of symmetry. If skewness is between 0 5 and 0 5 the distribution is approximately symmetric. Here x is the.

If skewness is between 1 and 0 5 or between 0 5 and 1 the distribution is moderately skewed. Low kurtosis does not imply a flattened shape the beta 5 1 distribution has low kurtosis but is infinitely pointy. M 19 6 sd 2 54.